Типы грамматик и их свойства

Рассмотрим классификацию грамматик (предложенную Н.Хомским), основанную на виде их правил.

Определение. Пусть дана грамматика G = (N, T, P, S). Тогда

если правила грамматики не удовлетворяют никаким ограничениям, то ее называют грамматикой типа 0, или грамматикой без ограничений.

если
- каждое правило грамматики, кроме S
  e, имеет вид
  
  , где |
  |
  |
  |, и
- в том случае, когда S
  e
  P, символ
  
  S не встречается в правых частях правил,
то грамматику называют грамматикой типа 1, или неукорачивающей.

если каждое правило грамматики имеет вид A

, где A
N,

(N
T)*, то ее называют грамматикой типа 2, или контекстно-свободной (КС-грамматикой).

если каждое правило грамматики имеет вид либо A
xB, либо A
x, где A, B
N, x
T* то ее называют грамматикой типа 3, или праволинейной.

Легко видеть, что грамматика в примере 2.5 - неукорачивающая, в примере 2.6 - контекстно-свободная, в примере 2.7 - праволинейная.

Язык, порождаемый

грамматикой типа i, называют языком типа i. Язык типа 0 называют также языком без ограничений, язык типа 1 - контекстно-зависимым (КЗ), язык типа 2 - контекстно-свободным (КС), язык типа 3 - праволинейным.

Теорема 2.1. Каждый контекстно-свободный язык может быть порожден неукорачивающей контекстно-свободной грамматикой.

Доказательство. Пусть L - контекстно-свободный язык. Тогда существует контекстно-свободная грамматика G = (N, T, P, S), порождающая L.

Построим новую грамматику G' = (N', T, P', S') следующим образом:

1. Если в P есть правило вида A

0B1

1...Bk

k, где k

0, Bi

+e для 1

k, и ни из одной

цепочки

j (0

k) не выводится e, то включить в P' все правила (кроме A

e) вида

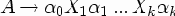
где Xi - это либо Bi, либо e.

2. Если S

+e, то включить в P' правила S'

S, S'

e и положить N' = N

{S'}. В противном случае положить N' = N и S' = S.

Порождает ли грамматика пустую цепочку можноо установить следующим простым алгоритмом:

Шаг 1. Строим множество N_0 = N | N

Шаг 2. Строим множество N_i = N | N

Ni - 1*

Шаг 3. Если N_i = N_i-1, перейти к шагу 4, иначе шаг 2.

Шаг 4. Если S

Ni, значитS

e.

Легко видеть, что G' - неукорачивающая грамматика. Можно показать по индукции, что L(G') = L(G). __

Пусть Ki - класс всех языков типа i. Доказано, что справедливо следующее (строгое) включение: K3

K0.

Заметим, что если язык порождается некоторой грамматикой, это не означает, что он не может быть порожден грамматикой с более сильными ограничениями на правила. Приводимый ниже пример иллюстрирует этот факт.

Пример 2.8. Рассмотрим грамматику G = ({S, A, B}, {0, 1}, {S

AB, A

0A, A

0, B

1B, B

1}, S). Эта грамматика

является контекстно-свободной. Легко показать, что L(G) = {0n1m|n, m > 0}. Однако, в примере 2.7 приведена праволинейная грамматика, порождающая тот же язык.

Покажем что существует алгоритм, позволяющий для произвольного КЗ-языка L в алфавите T, и произвольной цепочки w

T*

определить, принадлежит ли w языку L.

Теорема 2.2. Каждый контекстно-зависимый язык является рекурсивным языком.

Доказательство. Пусть L - контекстно-зависимый язык. Тогда существует некоторая неукорачивающая грамматика G = (N, T, P, S), порождающая L.

Пусть w

T* и |w| = n. Если n = 0, т.е. w = e, то принадлежность w

L проверяется тривиальным

образом. Так что будем предполагать, что n > 0.

Определим множество Tm

как множество строк u

T)+

длины не более n таких, что вывод S

*u имеет не более m шагов. Ясно, что T0 = {S}.

Легко показать, что Tm можно получить из Tm-1

просматривая, какие строки с длиной, меньшей или равной n можно вывести из строк из Tm-1

применением одного правила, т.е.

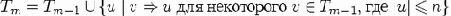
Если S

*u и |u|

n, то u

Tm для некоторого

m. Если из S не выводится u или |u| > n, то u не принадлежит Tm ни для какого m.

Очевидно, что Tm

Tm-1 для всех m

1. Поскольку Tm зависит только от Tm-1, если Tm = Tm-1, то Tm = Tm+1 = Tm+2 = ... . Процедура будет вычислять T1, T2, T3, . . . пока для некоторого m не окажется Tm = Tm-1. Если w не принадлежит Tm, то не принадлежит и L(G), поскольку для j > m выполнено Tj = Tm. Если w

Tm, то S

*w.

Покажем, что существует такое m, что Tm = Tm-1. Поскольку для каждого i

1 справедливо Ti

Ti-1, то если Ti

Ti-1, то число элементов в Ti по крайней мере на 1 больше, чем в Ti-1. Пусть |N

T| = k. Тогда число строк в (N

T)+ длины меньшей или равной

n равно k + k2 + ... + kn

nkn. Только эти строки могут быть в любом Ti. Значит, Tm = Tm-1 для некоторого m

nkn. Таким образом, процедура, вычисляющая Ti для всех i

1 до тех пор, пока не будут найдены два равных множества, гарантированно заканчивается, значит, это алгоритм. __

Содержание раздела